[논문 요약] AHP 응용 논문 (부동산 선택 ) 요약 및 정리

논문 정보

Using the Analytic Hierarchy Process in House Selection
J’NOEL BALL and VENKAT C.SPRINIVASAN (1994) Journal of Real Estate Finance and Economics, 9:69-85 

 

논문 요약

요약

주택 선택 시 협상 전에 구매자는 다양한 질적, 양적 요소를 평가함. 복잡한 정보들을 체계적으로 고려하기에 인간은 한계를 가지므로 이러한 요소들 간의 복잡한 상호 작용으로 인해 의사 결정에 있어 합의가 어려울 수 있음. 본 논문에서는 AHP를 이용한 주택 선정 과정의 형식적 판단 모델을 제시하며, 이 모델을 통해 구매자는 부동산 속성을 일관되게 평가할 수 있음.

 

0. 서론

* 주택을 구입하기 전에 구매자의 선호도를 엄격하게 정의하고 적용하기 위한 공식적인 모델이 
필요
∙ "매수자는 거짓말쟁이"라거나 "매수자는 논리가 아닌 감정으로 매입한다"는 말
∘ 이는 주택 구매자들이 특정 제약을 충족시키는 부동산만을 보여줄 것을 요구하지만 결국 
그러한 요구를 포기하는 집을 사게 된다는 관찰에서 비롯된 말

 

* 주택 구입 희망자는 결정을 내리기 전에 다양한 정보를 평가해야 하는 과제에 직면해 있음
∙ “3개의 침실, 2개의 욕실을 갖춘 단독 주택”으로 제한하더라도 대도시에서는 해당 조건을 만
족하는 sample이 매우 많음
∙ 구매자는 그러한 모든 부동산 데이터를 수집해야 함
∙ 주택별 자료를 꼼꼼히 수집했더라도 매수자는 각 부동산과 관련된 여러 특성을 평가해야 함
∘ 구매자의 입장에서 정보가 과부하된 상태에서는 평가 시 다양한 속성을 일관성이 없거나 
부적절하게 평가할 가능성 있음
∙ 최종 선택의 순위를 매기기 위한 목적 및 계약 과정 모두를 위해 부동산 속성에 대한 판단적 
평가를 listed된 가격과 통합해야 함
* 본고에서 구상하는 주택 선택과정
∙ 1단계 : 구매자의 극단적인 선호도를 적용하여 주택의 넓은 universe를 축소
∙ 2단계 : 본 논문에서 다루는 단계. AHP 모델을 통해 부동산 속성을 일관되게 평가함. 기본 
AHP 모델을 확장하여 구매자는 속성의 평가를 집값과 명시적으로 통합하여 속성 가중 가격
을 산출. 이는 사용자가 경쟁 주택의 순위를 매길 수 있도록 함

 

1. The Analytic Hierarchy Process

* AHP는 질적 기준을 체계적으로 평가하기 위한 매력적인(appealing) 방법론
∙ Saaty(1980)가 pioneer ∙ 다속성 의사결정 기법 (mutliattribute decision models; MADM)의 한 종류
∙ 여러 개의 기준들의 상대적 중요성을 정하는 과정을 통해 갈등을 해결하고 판단을 분석함
∙ 방법론은 “tradeoff”의 개념을 기반으로 하며, 의사 결정자는 일련의 상호 쌍별 비교 행렬을 
구조화하고 분석하는 과정에서 암시적으로 트레이드오프를 개발할 수 있음
* AHP의 세 가지 주요 구성 요소
∙ ① 주요한 문제는 계층적인 구조로 분해 가능함
∘ 각 level은 elements의 집합으로 구성되며 각 element는 다음 level의 계층을 위한 subelements로 분할됨
∘ final level은 의사결정 시 고려해야 할 특정 action으로 구성됨
∘ 장점 - 모든 문제를 계층적으로 구조화 ☞ 복잡성을 처리하고 문제의 관련 요소를 식별하기에 
효율적이고 직관적
- 의사 결정자가 개인의 요구와 선호도에 맞게 계층을 구성할 수 있도록 유연함
- 집단 의사 결정 설정 시 AHP를 사용하면 의견 불일치 영역을 정확히 파악 가능 ☞ 합
의를 달성하기 위해 이러한 영역에 더 관심 집중 가능
∙ ② 각 계층 level에서 다양한 elements에 대해 측정 scale을 사용해 상대적 가중치를 설정
∘ 아래의 9점 척도를 사용하여 특정 level의 element를 쌍으로 평가함. 하나의 element가 
같은 level 상에 있는 다른 element를 dominate하는 정도를 나타냄 - 1 : 두 요인 간 중요도에 차이 없음
- 3 : 하나의 요인이 다른 하나보다 weakly 더 중요
- 5 : 하나의 요인이 다른 하나보다 moderately 더 중요
- 7 : 하나의 요인이 다른 하나보다 strongly 더 중요
- 9 : 하나의 요인이 다른 하나보다 absolutely 더 중요

 

∙ ③ pairwise comparison matrices는 측정 이론을 사용해 평가됨
∘ 상대적인 dominance를 pairwise comparisions(쌍대비교)를 통해 측정함
∘ ex. n개의 속성 집합을 쌍으로 비교하고 상대적인 weights를 설정하는 경우
- 속성은 각각

로 표현
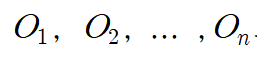
- 이들의 상대적 중요성은

로 표현
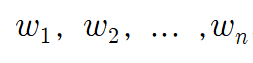
- 비교 행렬 (comparison matrix) O 는 아래와 같이 표현됨

- 이때

는 요소 j에 대한 요소 i의 상대적 중요성을 반영
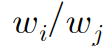
- 이하 자세한 행렬 계산 관련 선형대수 내용은 문헌 참고

 

2. The AHP and House Selection
2.1 AHP를 기반으로 한 주택 선택 모델

* 본 모델은 그림 3과 같은 계층적인 구조가 필요함
∙ ① Higher order 요인 (로마 숫자) ∙ ② lower order 요인 (알파벳 대문자) ∙ ③ 요인의 subdivision (아라비아 숫자와 알파
벳 소문자)
 ∙ 그림 4와 같은 계층 구조를 통해 의사결정 시 
선호하는 부분을 분명히 표시할 수 있음
* 계층을 평가하기 위해 1부터 9까지의 scale을 사
용하여 각 특성을 다른 것과 비교 가능
∙ Table 1 다시 보기
* 이후 구매자는 자신의 선호도가 높은 곳의 가격 범위에 해당하는 부동산을 찾음
∙ 집을 둘러보면서 계층 중 가장 높은 level의 요소에 주어진 순위와 가중치를 수정 가능
∙ 구매자는 2차 속성과 관련하여 집을 평가하여 최종 집합에서 각 주택의 순위를 매김
∙ 측정 프로세스를 통해 고려 중인 각 특성에 대한 2차 속성에 대한 전역 가중치를 도출. 계층적 가중치 체계는 관심 있는 대안에 대한 전체 가중치를 산출. 
∙ 각 속성에 대해, 우리는 최종 결과를 속성의 만족도 또는 바람직하지 않은 지표로 설명
∙ 그런 다음 만족도 가중치를 부동산 가격과 통합하여 후속 그림처럼 속성 가중치 산출 가능

2.2 예시

* first order attributes

∙ 첫 번째 레벨의 속성으로 ①접근성(Proxima), ②커뮤니티(Community), ③이웃 (Neighborhood), ④건물(Property)을 꼽았고, 이를 이용하여 서로 다른 것을 쌍으로 평가함

∙ community / neighborhood / property는 proxima보다 각각 weak (3), moderate (5), strong (7)만큼 dominance 가짐
∙ neighborhood와 property는 서로 거의 비슷한 dominance 가짐

∙ neighborhood와 property의 global weights는 각각 0.41, 0.40으로 매우 높은 편 => 이웃과 건물을 중요하게 생각함
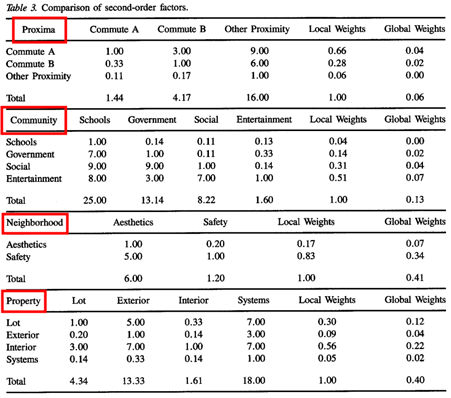
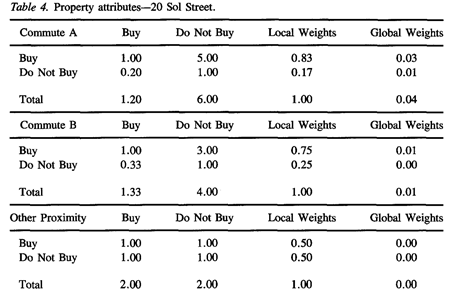
* second order attributes (red box)

 ∙ member A의 통근은 member B의 통근, 다른 시설로의 접근성에 비해 weak하게(3), absolute하게(9) 중요

 ∙ local weights를 합하면 1.00이 됨. local weights에 해당 첫번째 계층의 global weights를 곱하면 subelements의 global weights를 계산할 수 있음. => 다른 subelements와도 비교가 가능함

 

* 구매자의 선호도 확인
∙ 탐색 범위 a) 단일 가족 단독 주택, b) 경전철 시스템 도보 내, c) 수요가 많은 도시 d) 230,000달러 미만의 가격. 이러한 제한조건을 만족시켜야 함 ☞ Riverside rail line을 따라 Newton 시의 마을로 좁혀짐
∙ 부동산 투어 후 솔 스트리트 20번지와 보일스 로드 15번지 두 곳으로 추려짐
∙ 해당 부동산에 대한 각 2차 속성을 평가하면서 해당 부동산에 대한 최종 사전 오퍼 투어 수행
∙ 등급의 결과는 표 4와 5와 같음. 솔 스트리트 20번지의 전체적인 global weight는 0.89이고 15 보일스 로드는 0.55이므로, 이 가중치로만 생각하면 솔 스트리트 20번지를 구매하는 것이 합리적

 

 

 

2.3 Attribute Weighted Price (속성 가중 가격) 

 

* 속성가중치를 실현하기 위해서는 주택에 대한 판단가중치와 상장가격을 통합해야 함
∙ 추정치 : AWP (Attribute Weighted Price) = 구매에 대한 가격 / 글로벌 가중치
* 솔스트리트 주택의 가격 = 22만 5천 달러, 보일스로드 주택의 가격 = 20만 5천 달러, but 가중치 부여 가격은 각각 253,000달러(22만 5천 / 0.89)와 373,000달러 (20만 5천 / 0.55) 

∙ 만약 global weights가 1이라면 무지 좋은 집이며, 액면가 그대로 나에게 받아들여진다. 

∙ 좋지 않은 집일수록 가격이 높아진다. 

* 구매자는 처음에는 낮은 가치에 놀랐지만 계층 구조를 생각해본 후, 주택의 상태에 너무 많은 
가치를 두고 있다는 것을 깨달았고, 이웃에 대해서는 크게 생각하지 않았음을 알게 됨. => 보일스로드 15번지를 구매함

 

3. Aggregation of AHP Judgments

* 이전 섹션에서는 의사 결정자 또는 전문가가 한 명인 경우만을 고려함
∙ 그러나 현실적으로 판단이 서로 다르다면 여러 판단을 결합하는 집계 문제(aggregation problem)가 발생
∙ policy variables(objectives, criteria) 대한 상대적 우선 순위, 또는 대안적 조치 과정에 대한 글로벌 우선 순위 대한 의견이 앞에서 식별한 재정적 결정의 맥락에서 다를 수 있음
∙ 집계 문제의 두 가지 차원
∘ 전문가들 간의 공감대 형성 필요 ∘ 전문가의 판단이 적절한 통계적 방법론을 사용하여 수치적으로 집계되어야 함. 두 번째 차원은 합의에 도달하기 위한 시도가 이루어진 후 상당한 차이가 지속되는 경우에도 관련될 수 있음

 

3.1 합의 형성

 

* 전문가의 판단 사이에 큰 차이가 있을 때, 전문가들이 상호 작용하도록 함으로써 일부 차이 제거 가능
* 이때 상호 작용을 용이하게 하기 위한 여러 방법 있음
∙ 델파이 방법(Dalkey, 1969; Linstone and Turoff, 1975) : 가장 널리 알려진 방법
∘ 전문가들이 초기 추정치의 평균, 중위수 등 전문가의 초기 추정치를 바탕으로 그룹 요약에 
비추어 판단을 수정할 수 있도록 하는 것
∘ 의견 일치가 이루어지거나 더 이상의 의견 차이를 줄일 수 없을 때까지 수정 과정 계속
∙ 샹 인콰이어러(Ford, 1975) : 델파이 방법의 변형
∘ 일부 기준점에 상대적인 추정치의 실제 값의 위치에 대한 전문가의 판단을 나타내기 위해 
이진 응답 대안에 의존하며, 기준점은 전문가의 모달 응답을 사용하여 결정됨
∙ 두 방법 모두 합의에 대한 내재된 편견이 있다는 이유로 비판 받음
∘ 몇몇 저자들은 전문가에게 보다 질적인 피드백을 제공하는 대체 방법을 제안 (예: 
DeGroot, 1975; Chatterjee and Seneta, 1977; and Press, 1978 참조). 이러한 방법
의 대부분은 행동적 고려에서 비롯된 이론적 체계이며 적용하기 어려움

 

3.2 수치적 aggregation

* 반드시 공감대를 형성하려는 욕망이 없는 경우 존재. 전문가들 간의 상호 작용 후에도 판단 차
이 지속될 수 있음

∙ 전문가의 판단을 수치적으로 집계하기 위한 통계적 방법이 필요

∙ ① 산술평균 : 전문가들 간의 상호 작용이 없었던 경우를 고려

∙ ② trimmed mean : 

 

∙ ③ one-trimmed mean

∙ ④ two-trimmed mean

 

 

4. 결론

* AHP는 여러 정성적 및 정량적 속성에 기반한 일관성 있고 공식화된 결정을 내리는 데 강력한 도구
* 주택 선택은 매우 중요한 결정이지만 일반적으로 사용되는 프로세스는 naive하고 체계적이지 않음
* 본 논문은 구매자가 구매 가능 부동산을 순위 매길 때 AHP가 구매자가 보다 체계적이고 일관된 결정을 내리는 데 어떻게 도움이 되는지 보여줌. 또한 구매자가 협상하는 것을 돕기 위해 모델을 weighting of prices로 확장
* 판단에서 작은 동요의 영향을 확인하고 계층에서 다양한 수준 간의 피드백 관계를 허용하는 영향을 평가하기 위해 확장되고 있음
* 제시된 모델은 부동산 포트폴리오 관리, 부지 선정 및 주택담보대출 인수 분야에 적용 가능